Доказательство четвёртого признака равенства прямоугольных треугольников
Формулировка
Четвёртый признак равенства прямоугольных треугольников — если
Доказательство
Один из треугольников отразим и совместим треугольники равными катетами.
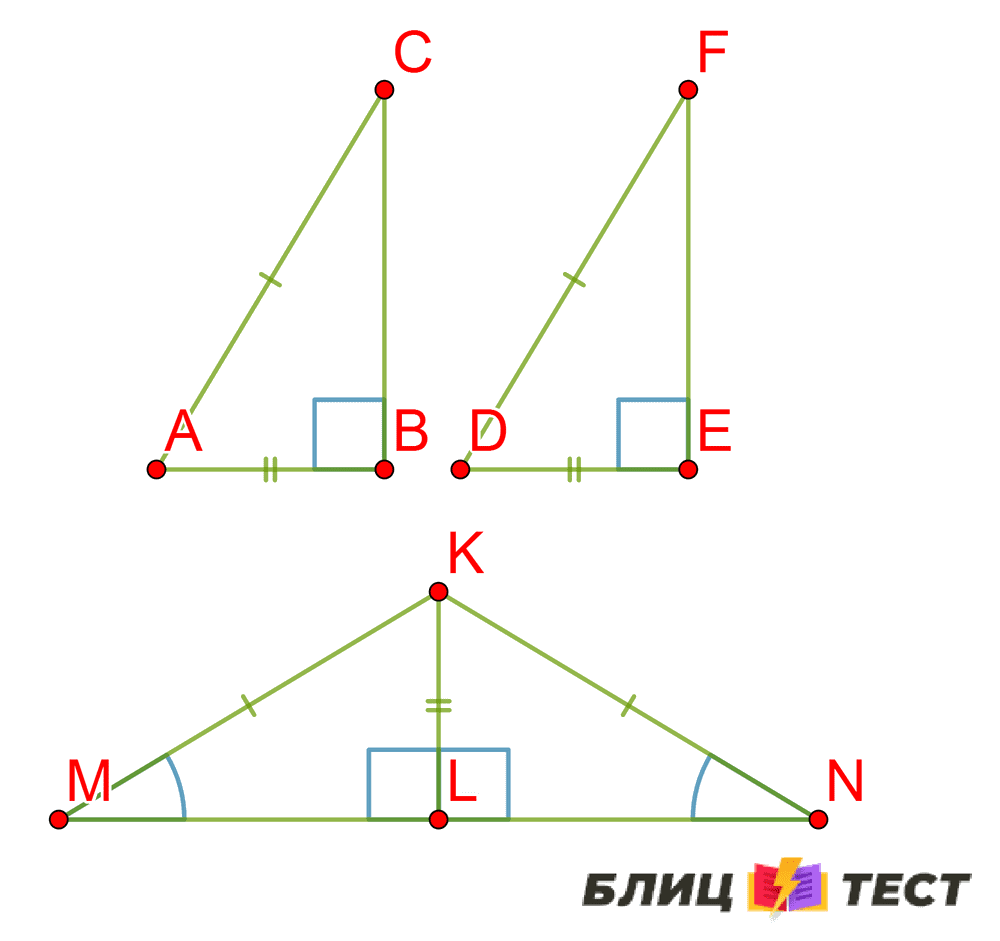 Доказательство четвёртого признака равенства прямоугольных треугольников
Доказательство четвёртого признака равенства прямоугольных треугольников
У этого треугольника две стороны равны MK=NK, следовательно треугольник KNM —
Выходит, что изначальные два треугольника равны по гипотенузе и острому углу, то есть по третьему признаку равенства прямоугольных треугольников. Что и требовалось доказать.