Третий признак равенства треугольников
Формулировка
Третий признак равенства треугольников — если три
Доказательство
Соединим подвинем, повернём треугольники равными сторонами AC и A1C1. Один из треугольников отразим сверху вниз. Затем соединим точки B и B1
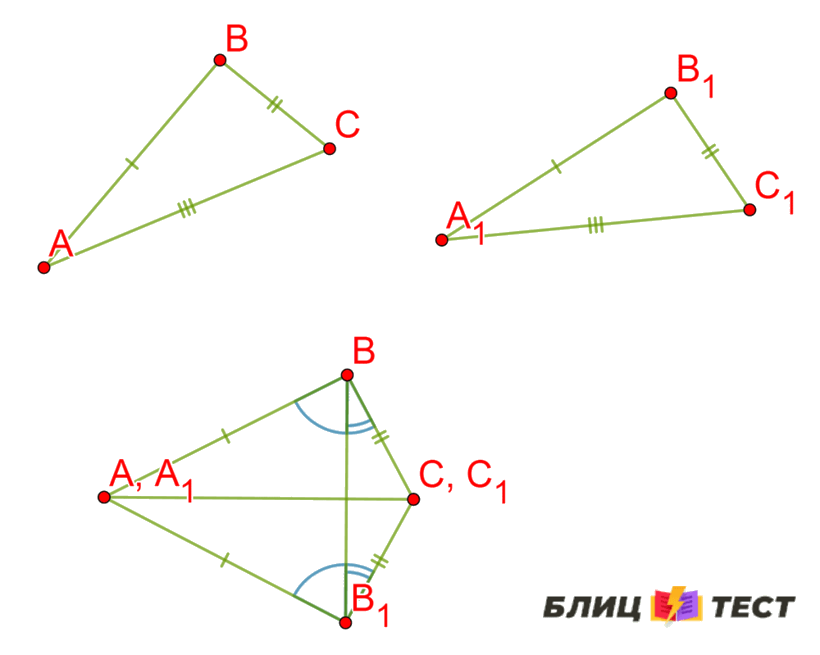 Первое доказательство третьего признака равенства треугольников
Первое доказательство третьего признака равенства треугольников
В треугольнике ABB1 стороны AB и AB1 равны. Следовательно треугольник ABB1
В треугольнике CBB1 стороны CB и CB1 равны, следовательно треугольник CBB1
У нас получилось, что углы ABC и A1B1C1 равны, так как они сложены из одинаковых углов. И следовательно исходные треугольники равны по двум сторонам и углу между ними. Что и требовалось доказать.